Challenge
You can’t see the flag.. but you can follow its track.
The download is an archive with a readme and a text file. In the readme we get a bit more information about the challenge:
This archive contains a sanitized execution trace of:
./flag-hunting-bin FLAG.txtThe trace is for debugging purpose only. The address of each instruction has been replaced with a unique identifier and our secure technology ensure that no data can be recovered from this trace.
– The OOO Secure Tracing Department
The text file is an execution trace of the flag-hunting-bin, but it only contains an obfuscated program counter, and the disassembled machine instruction. No memory contents, no register contents. The first few lines look like this:
3cda655ffeabac454f0ddeffbd60f3f3 mov r9,rdx
be8924b72ff3c6befe76ff77d13fe361 pop rsi
7bca8934003b83d64e73593c937f9a76 mov rdx,rsp
99a1ff7893c9a395d1331f630be96516 and rsp,0xfffffffffffffff0
bac8c7972748dded67677f6b80477780 push rax
7b00642b2afad3cf82d044a0a03ecf16 push rsp
The objective is clear: we have to obtain the flag from the execution trace, by inferring values from branches. But since we are lazy, we use tools for this. First of all, we transform the text trace into something more useful, and load it into TRCView. Since most people probably never heard about TRCView, a quick explanation about the tool.
TRCView
TRCView is an open source interactive execution trace analysis tool. It is architecture agnostic, so it can be used to analyze traces from all kinds of different architectures. It even supports a generic trace file format, which encodes information about the architecture in the file header. This is exactly what we will use for the flag-hunting challenge.
When loading an execution trace, TRCView reconstructs the memory contents for every point in time, tracks register values, and parses the instruction trace into a tree, where every level corresponds to a subroutine. This makes it convenient to analyze individual subroutines, without being overwhelmed by all the instructions from nested calls.
Since our execution trace only consists of obfuscated program counter values and decoded machine instructions, we use the generic trace file format. Every instruction gets a “step number”, which is the line number in the original trace - 1. Since the program counter for TRCView has to be at most a 64bit integer, we just generate new program counter values using the hashes. Generic trace files need information about the instruction types, so we parse the instruction mnemonic and assign the instruction type to every parsed instruction. The instruction type tells TRCView if it is looking at a jump/call/return/conditional branch/syscall/…; as machine code we just use the original obfuscated program counter value.
The main features of TRCView for analyzing the trace file of this challenge are subroutine names, comments, and instruction coloring. By renaming subroutines, we can easily understand what we are looking at, by adding comments, we can understand what the program code does, and by coloring instructions, we can quickly see loops and branches.
Analyzing the Trace
After loading the converted trace file into TRCView, we immediately see the first few instructions of the program.

The first call seems to go into the standard libc initialization function, which then calls the program’s main function with an indirect call (call rax), followed by a call to exit with the value returned by main. The main function therefore starts at instruction 214 (line 215 in the original trace file).
We can also see that many syscalls are performed over the program run. The first step now is to look at every syscall and annotate it with its name. For example this syscall:
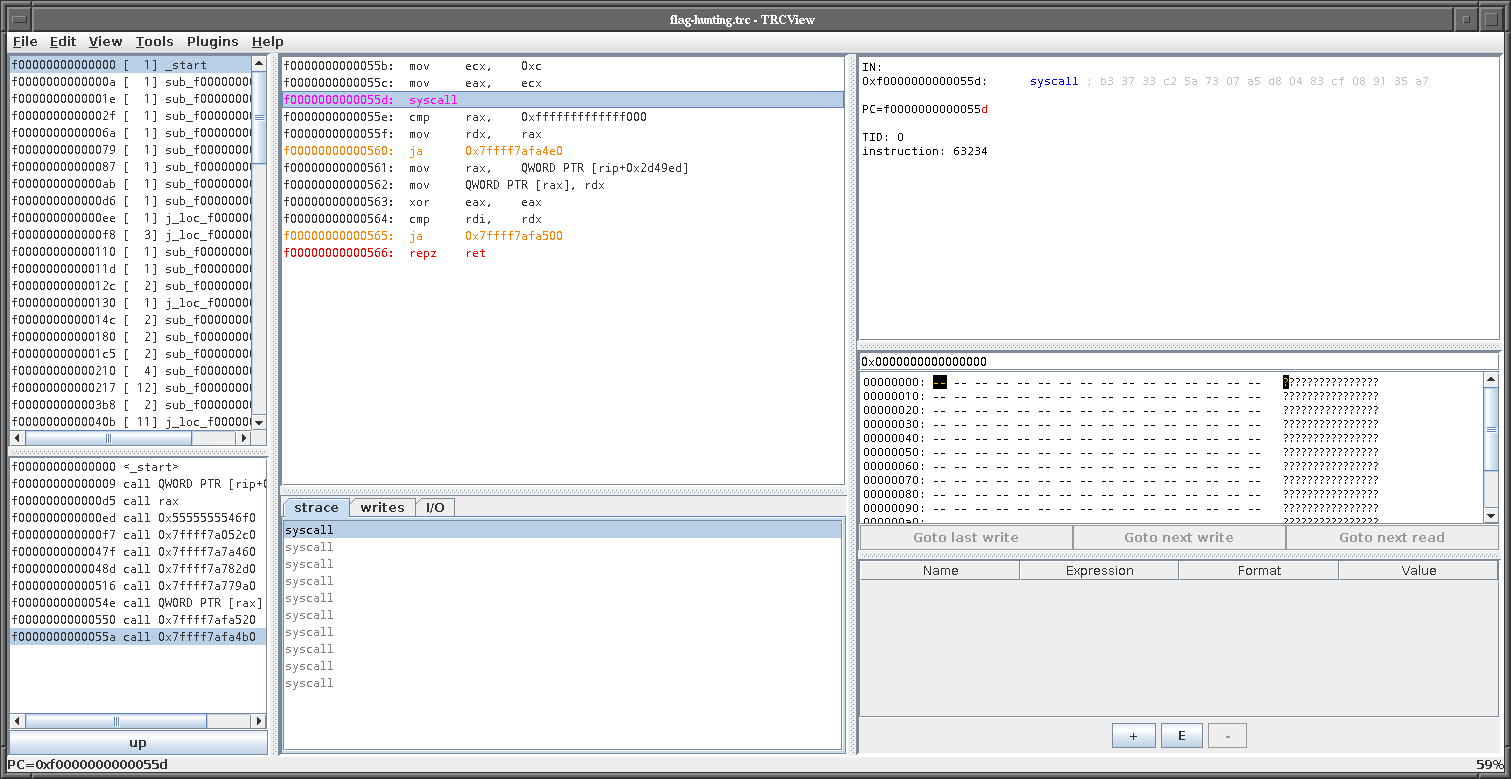
We can see the instruction moving a value of 0xC to eax, which means it is syscall 12 = brk. By adding brk as comment to the syscall instruction, we see it in the strace view too. After annotating all syscalls, we get an idea what happens over time:
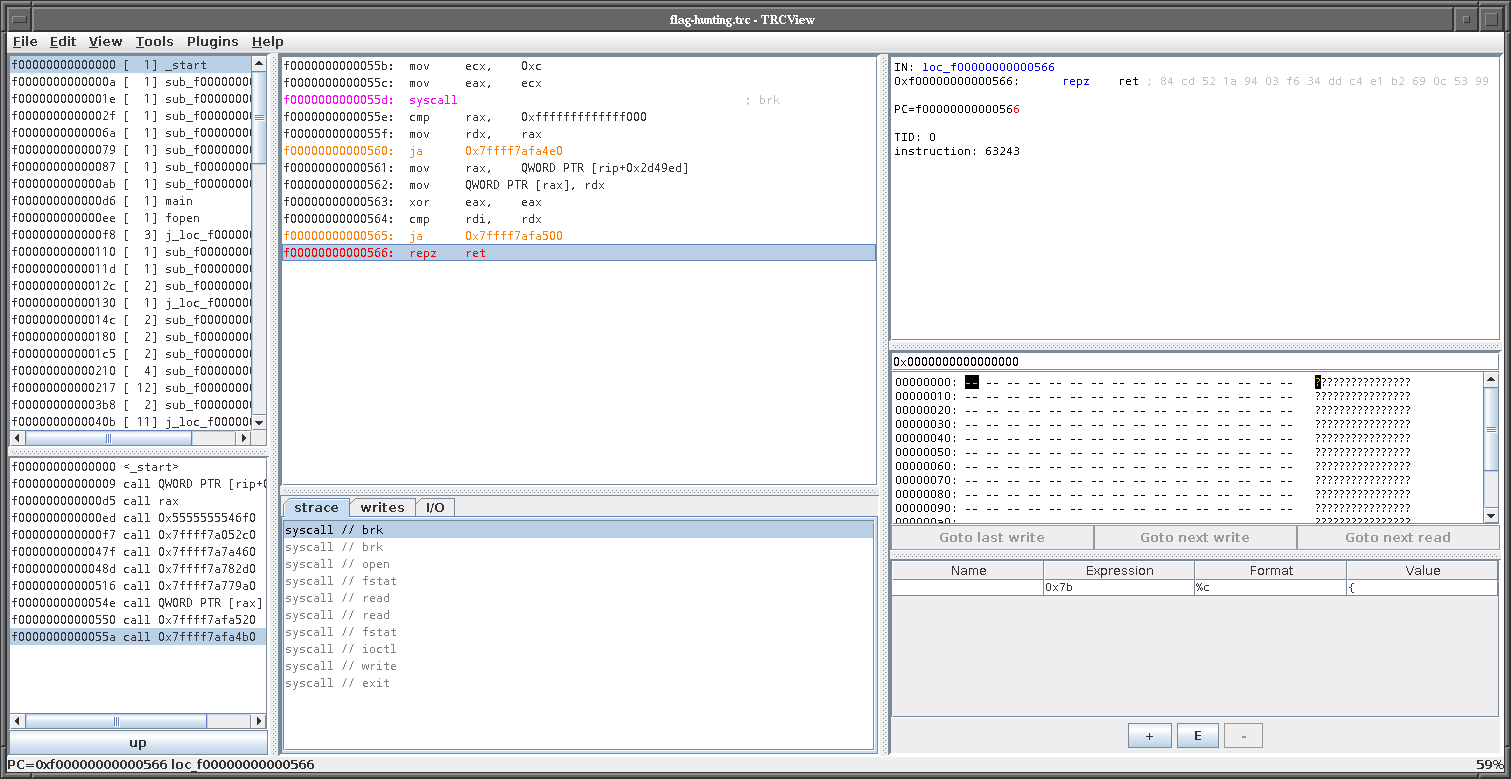
The program allocates memory, opens a file, reads content from a file, writes to some file, and then exits. By going up the call stack from every syscall, we can recover the libc function names. For example the open syscall is eventually called from fopen, read is eventually called from fread, and so on.
The main function
The program’s main function looks roughly like this:
int main(int argc, char** argv)
{
char flag[60];
memset(flag, 0, sizeof(flag));
FILE* f = fopen(argv[1], "rt");
fread(flag, 1, sizeof(flag), f);
int flag_len = check_flag_format(flag);
process_flag(flag, flag_len);
return 0;
}
The two interesting functions now are check_flag_format and process_flag. Let’s look at check_flag_format.
Flag Format Check
This flag format check verifies if the characters in the flag are valid and at the same time it computes the flag length. Since this code specifically checks for O, space, and character value ranges, we know that the flag starts with three O characters, there are space characters in the flag, and all other characters are greater than 0x60, which means it’s all lowercase letters. With this information, we can now look at the subroutine which processes the flag.
Processing the Flag
The process_flag subroutine allocates three variables, one is the pointer to the flag buffer, the second one is a counter, and the last one is another 64bit value initialized with NULL. The code then iterates over all characters of the flag, and calls a function with the 64bit value and the character from the flag. The returned value replaces the 64bit variable’s value. This means the new function updates this value somehow.
Essentially the code so far looks like this:
void* ptr = NULL;
for(int i = 0; i < flag_len; i++) {
ptr = do_something(ptr, flag[i]);
}
Looking at the called function itself, it seems to create some data structure. In the first invocation, it creates a new element, in later invocations, it traverses the data structure and modifies it. Now we know the 64bit variable in the process_flag subroutine is actually a pointer to this data structure. Let’s rename this do_something to insert, because that’s probably what it does.
After the loop finishes, another function is called, which turns out to be a print function. The complete code of process_flag looks roughly like this:
void process_flag(char* flag, int flag_len)
{
void* ptr = NULL;
for(int i = 0; i < flag_len; i++)
ptr = insert(ptr, flag[i]);
print_data(ptr);
}
The insert operation
In the insert function, the first invocation creates a new node. The function which creates the node looks like this:
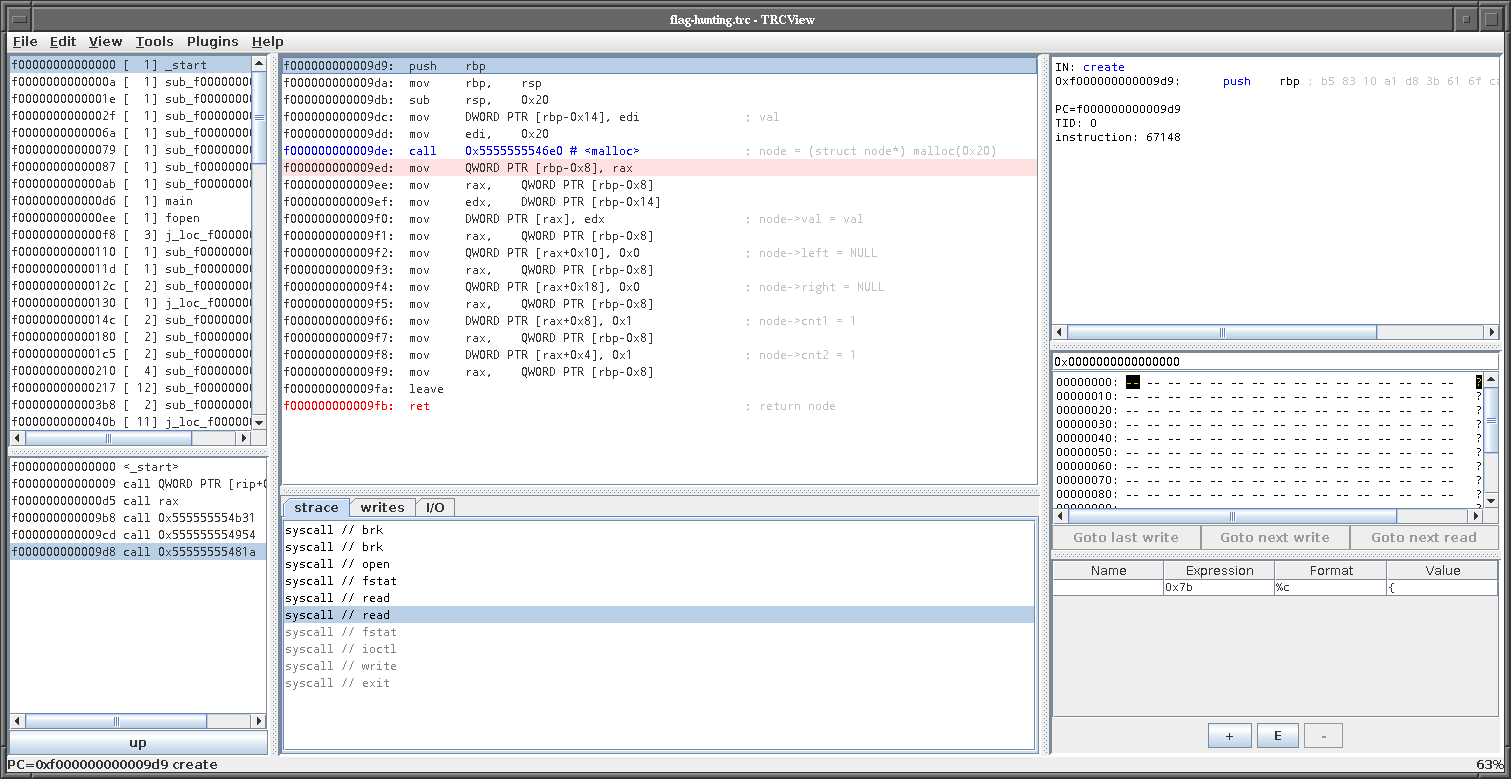
From here we learn that nodes are 32 bytes large, and have a structure like this:
struct node {
int val;
int cnt1;
int cnt2;
int pad;
struct node* left;
struct node* right;
};
The left and right can be inferred from the print function, which traverses this data structure:
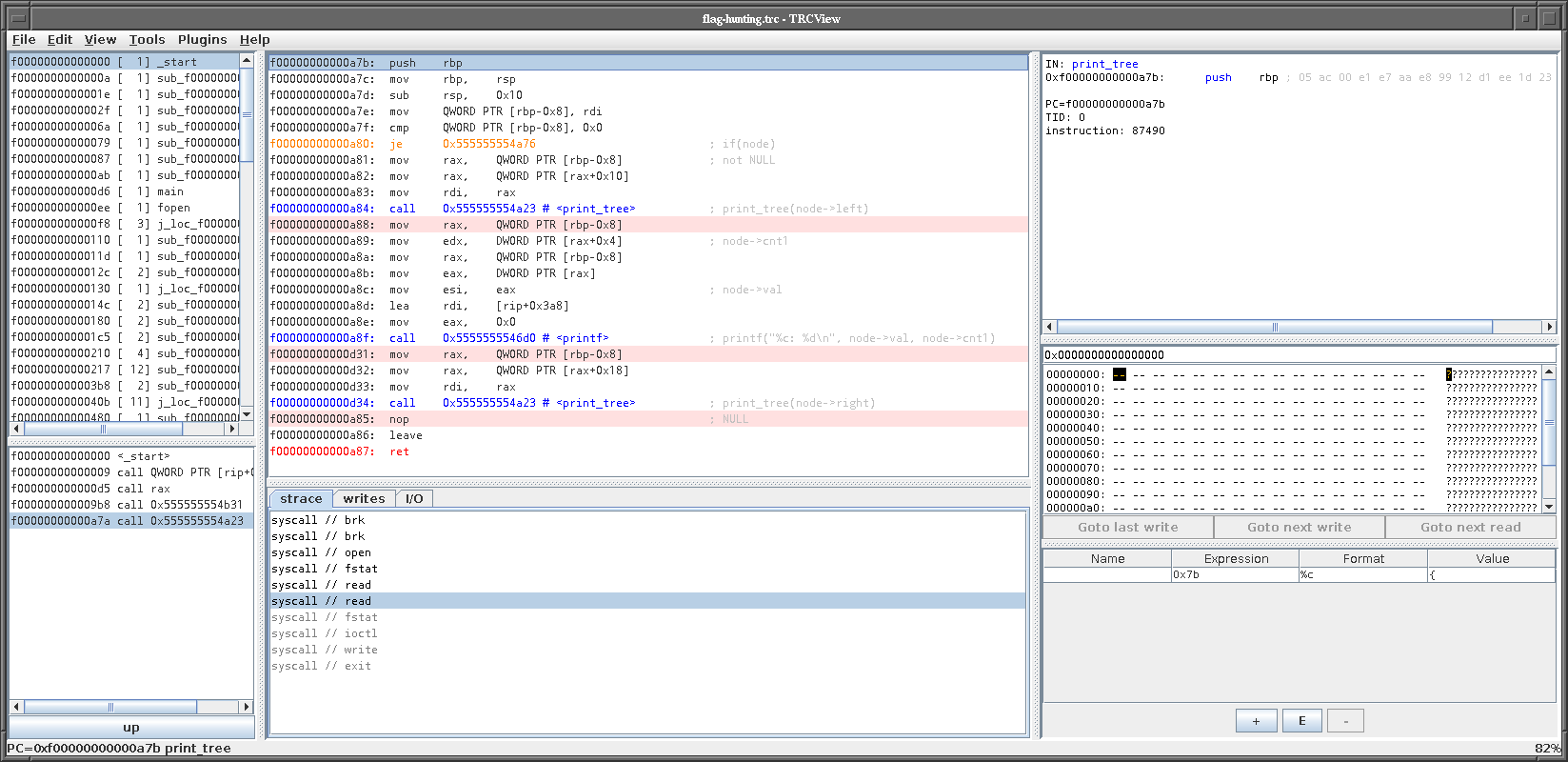
We can now safely assume it’s a binary tree, with the value, a left and right pointer, and two counters. The first counter is the number of occurences of the character. The decompiled version of the print_tree function from the screenshot looks roughly like this:
void print_tree(struct node* node)
{
if(!node)
return;
print_tree(node->left);
printf("'%c': %d\n", node->val, node->cnt1);
print_tree(node->right);
}
Basically the process_flag function counts the occurrences of every character in the flag. Although we cannot observe the values themselves, we can observe the position of the values in the tree, and since the flag has 21 unique characters (which can be guessed from the invocation count of create), guessing the rest should be easy.
Now we have to understand the rest of the insert function to get the character positions in the tree.
The first case for insert was to create a new node, since the passed node was NULL. The second case for insert looks like this:
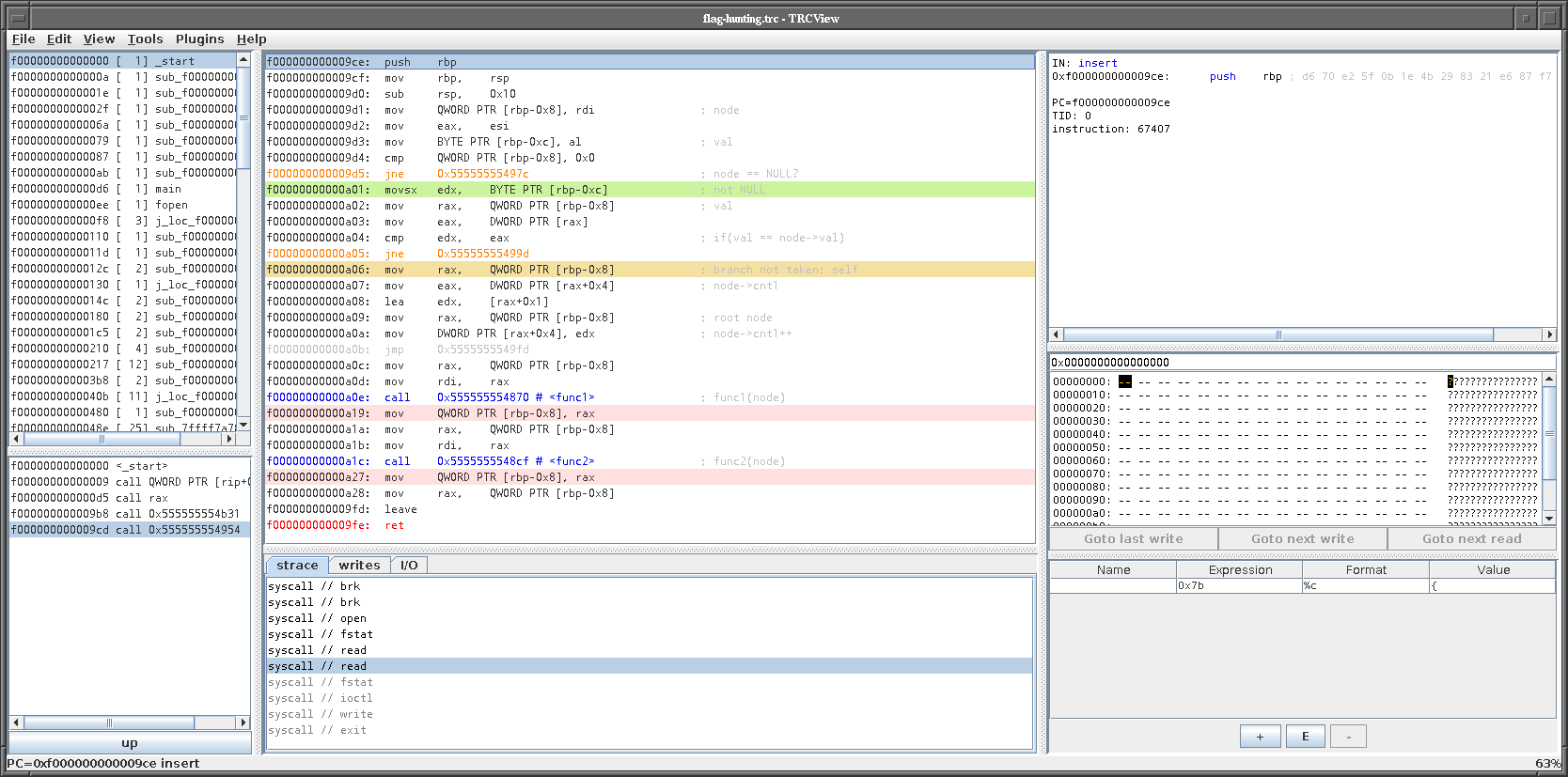
The node has the value that is to be inserted into the tree, so the first counter is incremented. Afterwards, two functions (func1 and func2) are called, which somehow re-organize the tree. In this specific case, they don’t do anything.
The third case of insert is for recursively inserting into one subtree, the fourth one recursively inserts into the other subtree. But the question remains, what does func1 and func2 do? Looking at all the invocations, func1 seems to do this:
struct node* func1(struct node* node)
{
if(node->left && node->left->cnt2 == node->cnt2) {
struct node* n = node->left;
node->left = n->right;
n->right = node;
return n;
} else {
return node;
}
}
The other function (func2) does something rather similar:
struct node* func2(struct node* node)
{
if(node->right && node->right->right &&
node->cnt2 == node->right->right->cnt2) {
struct node* n = node->right;
node->right = n->left;
n->left = node;
n->cnt2++;
return n;
} else {
return node;
}
}
Those functions seem to re-balance the tree. Now that we know how the tree is constructed, all we have to do is re-implement all those functions, re-play the trace and create a tree with exactly the same structure, but with the positions of the flag characters as content. To do this, we write a simple python script.
Decoding the Trace
Remember that TRCView shows the original obfuscated program counter addresses in the “machine code” comment? This is what we need now to decide in the python script what to do. The basic idea is to read the trace in the python script, check for (obfuscated) program counter values, and then perform some actions. We don’t care about the actual machine code at this point.
First of all, we read the trace file and only keep the obfuscated program counter value:
with open("trace.txt", "rt") as f:
data = f.readlines()
trace = [ int(x.split(" ")[0], 16) for x in data ]
Then we have to parse the trace of the check_flag_format function, which reveals the flag length:
def check_flag_format(trace):
i = 0
for step in trace:
if step == 0xcd97512d07efe7aa3271311a5a343e98:
i += 1
elif step == 0x9a5816982d4321860eb7bec0b5ae8d3e:
i += 1
elif step == 0xb42b799b2e1ef9ce91bf86738b6fa8fb:
return i
The next function is the process_flag function, which has to reconstruct the tree. The tree itself has a rather simple structure:
class Tree(object):
def __init__(self, val):
self.val = [ val ]
self.left = None
self.right = None
self.count = 1
self.cnt2 = 1
The function func1 is rather easy to implement in python, since it doesn’t even need to look at the trace at all:
def func1(node):
if node.left is not None and node.cnt2 == node.left.cnt2:
n = node.left
node.left = n.right
n.right = node
return n
else:
return node
The function func2 is similar, and again, it doesn’t need to check the trace:
def func2(node):
if node.right is not None and node.right.right is not None and \
node.cnt2 == node.right.right.cnt2:
n = node.right
node.right = n.left
n.left = node
n.cnt2 += 1
return n
else:
return node
Although those two functions don’t have to check the trace, the correctness can be verified by checking the trace. Since the decisions made in the python script have to match the decisions in the trace, it’s easy to see if there are any differences.
Now the insert function can be recreated:
def insert(trace, start, val, tree = None):
cont = None
for i in range(start, len(trace)):
if cont is not None: # continue if necessary
if cont > i:
continue
else:
cont = None
step = trace[i]
if step == 0x7e8d3d12f9987acc83634394bb225179:
tree = Tree(val)
elif step == 0x9fd18c435279a11cc106c4933676a7d9:
(_, cont, node) = insert(trace, i + 1, val,
tree.left)
tree.left = node
elif step == 0xa2648a849526903f1553126aa4119b79:
(_, cont, node) = insert(trace, i + 1, val,
tree.right)
tree.right = node
elif step == 0xb39fabb14ca48dfa222944f6b24fff4b:
tree.count += 1
tree.val += [ val ]
elif step == 0x83558aaf42e5b6c58859338ad3e67ec6:
tree = func1(tree)
elif step == 0x7dd2b7931b57d948b675c187dcdb0104:
tree = func2(tree)
elif step == 0x035619afe13a4b106de53674a406125f:
return (trace, i + 1, tree)
With insert implemented, we can now implement the function which creates the tree:
def create_tree(trace):
pos = 0
tree = None
for i in range(len(trace)):
step = trace[i]
if step == 0xca5ab312e8886c46a899368f61547e0b:
(_, _, tree) = insert(trace, i, pos, tree)
pos += 1
return tree
By calling create_tree on the trace, we get a reconstructed tree which has the character positions of the flag characters in the val field of the nodes. Now all we have to do is generate a flag out of this tree.
Generating the Flag
We need to serialize the tree into a set of equivalent characters, which we call classes from now on. Those classes represent different characters, and the most important property is that the character values of the classes are sorted from smallest to biggest value.
def serialize(tree):
if tree is None:
return []
result = serialize(tree.left)
result += [ tree.val ]
if tree.right is not None:
result += serialize(tree.right)
return result
Getting the classes is now easy:
tree = create_tree(trace)
classes = serialize(tree)
Now we can assign character values to every class. For the first two classes we already know the values: space and O. The last class is the { character.
values = [ '.' ] * len(classes)
values[0] = ' '
values[1] = 'O'
values[-1] = '{'
Unfortunately the character values are not value[i] = x + i, but instead there is a “gap” between some character values. This is what we have to guess. Solving the challenge is now about guessing those “gaps”:
skip = [ 0 ] * len(classes)
skip[7] = 2
skip[9] = 2
skip[14] = 1
skip[19] = 2
off = 0
for i in range(2, len(classes) - 1):
off += skip[i]
values[i] = chr(0x60 + (i - 1) + off)
flag = [ '}' ] * len(flag_format)
for i in range(len(classes)):
for n in classes[i]:
flag[n] = values[i]
print("".join(flag))
The complete solve script is available here: solve.py
Running this script reveals the flag:
OOO{even my three year old boy can read this stupid trace}
Other Observations
- The program was probably compiled with
-O0, since many useless load and store operations can be observed. - The program is dynamically linked, since GOT/PLT based calls can be observed, and two different address ranges are in use.
- The program was probably traced with a debugger, because the address range of the program code starts with 0x5555…
- The dynamic linker cannot be observed at any time, which indicates that all functions were resolved before the trace recording started.